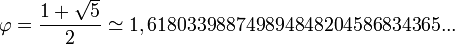
En effet, l'architecte qui construit un grand édifice inclut souvent des propriétés mathématiques d'actualité pour mettre en valeur ses connaissances scientifiques; par exemple, l'architecte qui a construit la Grande mosquée a ajusté la largeur et la longueur de son édifice au cm près pour que le rapport des cotés donne le nombre d'or :
.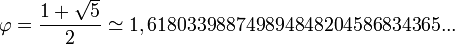
Une autre techniques très importante chez les maalems :

Le carré védique, issu de la tradition brahamique est intégré très tôt par l'Islam et associé à ses combinaisons ornementales. La première ligne horizontale et la première ligne verticale contiennent chacune les nombres de 1 à 9. On remplit les autres cases aves le produit des deux nombres correspondants, horizontalement et verticalement, comme avec une grille de mots croisés. Exemple : 7 x 9 = 63 ( 6 + 3 = 9). Ce carré est rempli de surprises mathématiques, à commencer par le chiffre 7 au "pouvoir magique", en son centre.
Les combinaisons du carré védiques se transmettaient dans les confréries d'initiés, comme celle des Frères de la pureté... En réunissant les centres des carrés d'un même chiffre, on obtient des figures géométriques qui différent selon que l'on réunissent les 1, les 2, ect. Ces figures, utilisées par superpositions et rotations forment des constrcutions au combinaisons multiples abondamment exploitées par les dessinateurs.
La lecture de la grille védique, en suivant chaque portée horizontale, permet la construction de figures à partir du cercle divisé en neuf parties égales (comme le carré lui même) :
1 - L'ennéagone en joignant les points 1, 2, 3, 4, 5, 6, 7, 8, 9;
2 - Le triangle équilatéral en joignant les points 3, 6, 9, 3, 6, 9, 3, 6, 9;
3 - Le sceau a neuf pointes en joignant les points 2, 4, 6, 8, 1, 3, 5, 7, 9;
4 - Létoile à neuf branches en joignant les points 4, 8, 3, 7, 2, 6, 1, 5, 9.
Le nombre infini de possibilité laisse donc un libre recours a l'imagination.


Il est probable que des procédés identiques furent encore employés par les artisans nasrides qui décorérent l'Alhambra, tant leurs compositions témoignent d'une inspiration originelle.
Il faut rappeler que le carré est toujours un principe de base dans les inventions des maalems. Sa persistance dans le décor rappelle ses origines symboliques et magiques:

Le rectangle d'or :
Cette partie sera expliqué à l'oral.De même il existe "le pavage de Penrose", il nécessite l'utilisation du *triangle d'or
Démontration :
 Chacun
de ces types possède un angle
Chacun
de ces types possède un angle  de 36 ° (soit
de 36 ° (soit  radians).oit
égaux à
radians).oit
égaux à  ,
soit multiples de
,
soit multiples de  (d'un facteur 2 ou 3).
L'angle
(d'un facteur 2 ou 3).
L'angle  est lié au nombre d'or φ par de nombreuses
propriétés ; en effet :
est lié au nombre d'or φ par de nombreuses
propriétés ; en effet :
 et
et

La propriété peut être
précisée de la façon
suivante :
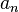 le nombre de triangles aigus et
le nombre de triangles aigus et  le nombre de triangle obtus, on observe les formules de
récurrence :
le nombre de triangle obtus, on observe les formules de
récurrence :suite dont on sait que le rapport de deux termes consécutifs tend vers le nombre d'or φ. Ainsi la valeur limite du rapport du nombre de triangles obtus et du nombre de triangles aigus est un nombre irrationnel, ce qui entraîne que le pavage obtenu de cette façon ne peut pas être périodique.
montrant comment on peut, avec des triangles d'or, réaliser un pavage de Penrose de type 0 (6 étapes) Penrose_pavage1_6_steps.gif